Shinoyuki
0%

Variational AutoEncoder

Posted on Edited on In

Variational AutoEncoder(VAE) 简单还是难？

理解优先，推导其次。
文末只有小段推导过程，其他的推导可以参考概率图模型相关文章，或通过其他网络资源获取。申明一下推导很重要，但有时候过于注重推导会陷入迷茫之中……

附代码（pytorch） DemoML/VAE_NLG/

本文中概率$p$表示随机变量概率分布，粗体小写表示单一数据的向量，下角标为样本编号，带括号上角标一般表示维度。变量表示规则和其他博文保持一致。

由于手写无法体现粗体，我一般选择变量加下横线表示一个向量。本文配图中，为了更清晰的展示，因此没有加下横线，实际都是向量。

VAE基本思想

VAE目标：最大化似然函数$p(\mathcal{D})$

VAE源于AutoEncoder（AE）是一个生成模型，目的是希望生成符合分布$p(\mathbf{x})$的数据。于是目标就是得到$\mathbf x$的分布$p(\mathbf{x})$。

然而当前我们手中只有观测数据$\mathcal D =\{\mathbf{x}_i\}^N_{i=1}$，是从$p(\mathbf{x})$中独立同分布(iid)采样N次得到的。我们假定$\mathbf x$可由隐变量$\mathbf z$生成，数学表达式为

其中$p(\mathbf{x}\mid \mathbf{z})$表示$\mathbf z$到$\mathbf x$的生成过程；$p(\mathbf{z})$表示隐变量$\mathbf z$的先验，我们先验假设$\mathbf{z}$服从标准正态分布$p(\mathbf{z})\sim \mathcal N(\mathbf{0},\mathbf{I})$。

现在模型基本构建完毕，目标就是学习$p(\mathbf{x}\mid \mathbf{z})$，使得边缘概率$p(\mathcal{D})=\sum \limits _{(i=0)}^N p(\mathbf{x}_i)$最大。

模型的目标函数用MSE(mean squared error)表示为 $\sum \limits_{i=1}^N (\mathbf{x}_i - \mathbf{\hat x}_i)^2$

图1. VAE模型生成数据
目标函数的问题

在训练中，上面的目标函数求解有一点小问题。根据VAE的定义，从$p(\mathbf{z})$的采样是随机的。于是通过随机采样得到$\mathbf{z})$生成的$\mathbf{\hat x}$就无法和$\mathcal D =\{\mathbf{x}_i\}^N_{i=1}$中的数据一一对应。因此无法实现$\sum \limits_{i=1}^N (\mathbf{x}_i - \mathbf{\hat x}_i)^2$中对应相减。

这点从图1中也可以看出来，数据$\mathcal D =\{\mathbf{x}_i\}^N_{i=1}$到$p(\mathbf{z})$其实不存在训练，丢掉了对应关系。

从模型定义角度分析问题原因：由于我们想从$\mathcal D =\{\mathbf{x}_i\}^N_{i=1}$得到全局的隐变量分布$p(\mathbf{z})$，因此$p(\mathbf{z})$并没有对单个数据$\mathbf{x}_i$存在对应关系。无法一一对应造成目标函数无法得到，从而导致无法训练。

简单粗暴，把对单个数据$\mathbf{x}_i$的对应关系加入隐变量分布$p(\mathbf{z})$中，数学表达为$p(\mathbf{z}\mid \mathbf{x}_i)$。然后我们从$p(\mathbf{z}\mid \mathbf{x}_i)$，采样得到的$\mathbf{\hat x}_i$，对应关系就建立起来了。从贝叶斯推断的角度理解：原本从先验分布采样$p(\mathbf{z})$，现在改为从后验分布$p(\mathbf{z}\mid\mathcal D)$采样，加入了对数据的依赖。

由于正态分布的各种优越特性，我们进一步假设后验分布$p(\mathbf{z}\mid \mathbf{x}_i)$为多元独立的正态分布，这个假设是为了便于计算，后面关于latent loss的analytic form可以看到好处。这一点在第一次提出VAE的论文Auto-Encoding Variational Bayes章节3有明确提到：

In this case, we can let the variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure（Note that this is just a (simplifying) choice, and not a limitation of our method.）

VAE模型的拟合过程

拟合后验分布$p(\mathbf{z}\mid \mathbf{x}_i)$

由于假设$p(\mathbf{z}\mid \mathbf{x}_i)$服从多元独立正态分布，根据正态分布特性，我们需要转化问题为拟合$\mathbf{\mu}$和$\mathbf{\sigma}$。没什么别的想法，就直接上神经网络。由于不加限制的神经网络输出范围为$(-\infty,+\infty)$，因此选择输出拟合$\log(\sigma_i^{2})$来保证方差为非负特性，表示为$f_1(\mathbf{x}^i)=\mu$,$f_2(\mathbf{x}^i)=]log(\sigma_i^2$，表达分布$q_\phi(\mathbf{z}\mid \mathbf{x}_i)$。其中$\phi$是变分参数

从后验分布中采样生成$\mathbf{\hat x}_i$

训练时从神经网络表达的分布$q_\phi(\mathbf{z}\mid \mathbf{x}_i)$中采样$\mathbf{z}_i$，然后通过生成模型(Generator)得到$\mathbf{\hat x}_i$。生成模型符合概率分布$p(\mathbf{x}\mid \mathbf{z})$，表示为$p_{\mathbf \theta}(\mathbf{x}_i\mid\mathbf{z})$。$\theta$是生成模型参数，这个生成模型一般会被称为probabilistic decoder，也可以由神经网络构成。

图2. VAE完整模型

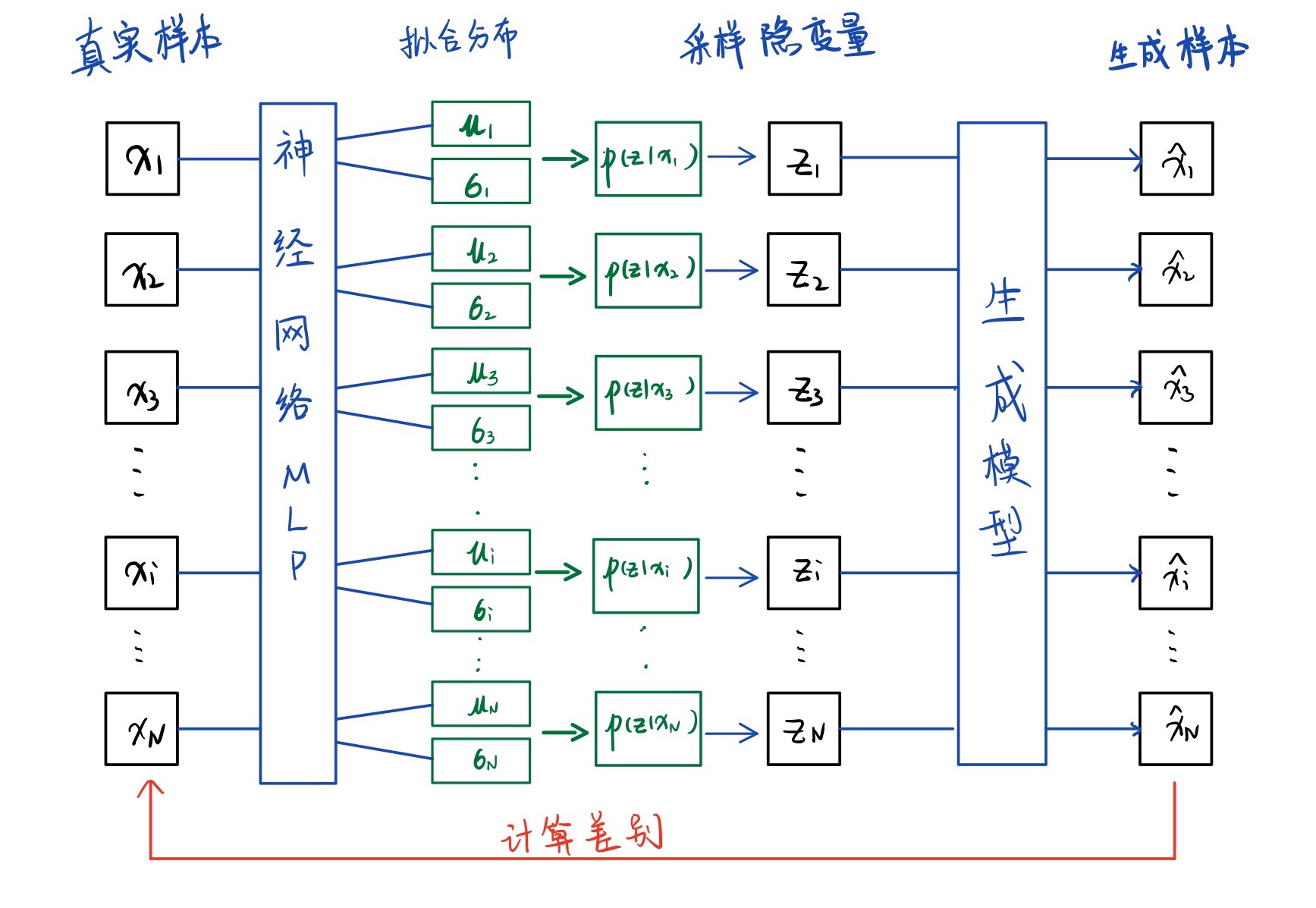
训练VAE

神经网络生成分布$q_\phi(\mathbf{z}\mid \mathbf{x}_i)$的loss计算

神经网络表达的分布$q_\phi(\mathbf{z}\mid \mathbf{x}_i)$希望尽可能接近真实分布$p(\mathbf{z}\mid \mathbf{x}_i)$，可用KL散度表示两个分布的距离为（推导过程在后面）：

目标是最小化等式左边的KL散度，当样本$\mathbf{x}_i$给定时，$\log p(\mathbf{x}_i)$为定值，无需考虑。这样就剩下两项内容$KL(q_\phi(\mathbf{z}\mid \mathbf{x}_i)\mid\mid p(\mathbf{z}))$和$-\mathbb{E}_{q_\phi(\mathbf{z}\mid \mathbf{x}_i) )}\log p(\mathbf{x}_i\mid \mathbf{z})$。目标简化为最小化$KL(q_\phi(\mathbf{z}\mid \mathbf{x}_i)\mid\mid p(\mathbf{z}))$和最大化期望$\mathbb{E}_{q_\phi(\mathbf{z}\mid \mathbf{x}_i) )}\log p(\mathbf{x}_i\mid \mathbf{z})$。

最小化$KL(q_\phi(\mathbf{z}\mid \mathbf{x}_i)\mid\mid p(\mathbf{z}))$

这式子一看我们应该高兴，因为前面先验假设$\mathbf{z}$服从标准正态分布，并且$q_\phi(\mathbf{z}\mid \mathbf{x}_i)$是多元独立正态分布。利用假设，此KL散度具有有analytical solution解（证明略）：

其中$J$是隐变量$\mathbf{z}$的维度，$j \in J$。

如何理解这个公式？这可以理解成图2左边神经网络的loss，其中$\mu_j$,$\sigma_j^2$都是神经网络的输出。

最大化期望 $\mathbb{E}_{q_\phi(\mathbf{z}\mid \mathbf{x}_i) )}\log p(\mathbf{x}_i\mid \mathbf{z})$

由于我们用生成模型表达$\mathbf{z}$到$\mathbf{x}$的生成过程，因此把模型参数加入期望中$\mathbb{E}_{q_\phi(\mathbf{z}\mid \mathbf{x}_i) )}\log p_\theta(\mathbf{x}_i\mid \mathbf{z})$。

最简单的想法是对该期望求导，导函数有close form表达（略，也许图模型博文会有涉及），但求解不太现实。

如何能更好的对采样过程求梯度呢？注意到这里导数难以求解的问题源于采样后验分布$\mathbf{z}_{i,l} \sim q_\phi(\mathbf{z}\mid \mathbf{x}_i)$。于是VAE作者提出一种巧妙采样方法：先从$\mathbf{\epsilon}_l \sim \mathcal{N}(0,\mathbf{I})$中采样，然后经过函数$g_\phi(\mathbf{\epsilon}_l,\mathbf{x}_i) = \mathbf{\mu}_i+\mathbf{\sigma} \odot \mathbf{\epsilon}_l$得到$\mathbf{z}_{i,l}$。

该过程采样得到的$\mathbf{z}_{i,l}$理论上和直接采样后验分布$\mathbf{z_{i,l}} \sim q_\phi(\mathbf{z}\mid \mathbf{x}_i)$一致。从数学简单理解为：如果$a$服从标准正态分布，那么$func(b) = \sigma a+\mu$表示均值$\mu$，方差$\sigma^2$的正态分布，这里的$func(b)$就是$g_\phi(\cdot)$。

我的理解是增加一个函数让随机采样过程变成了运算过程，线性运算过程是可解的。由于神经网络来对梯度运算的强烈依赖，必须要有一个可以微分的函数…

然后利用蒙特卡洛估计函数的期望如下

神经网络如何体现两部分最值

如果由神经网络替代图2中的所有拟合函数，那么第一个神经网络我们可以称为编码器encoder，第二个生成模型为解码器decoder。最小化$KL(q_\phi(\mathbf{z}\mid \mathbf{x}_i)\mid\mid p(\mathbf{z}))$可以理解为encoder的loss，表达encoder的拟合隐变量的能力。最大化期望 $\mathbb{E}_{q_\phi(\mathbf{z}\mid \mathbf{x}_i) )}\log p_\theta(\mathbf{x}_i\mid \mathbf{z})$可以理解为MLE或者最小化MSE，也就是一般神经网络计算loss的目标函数。

两者相加之后我们得到了神经网络目标函数+latent loss的表达形式，用于计算梯度。

后记

以上只是把VAE的过程说了一遍，其实VAE还存在很多巧妙的设计。比如正常的AutoEncoder也学习了隐变量，不同点在于VAE学习的隐变量不是条件于输入数据的定值，而是独立的一个分布，我们可以从该分布直接生成数据。也就是在inference阶段，我们只需要使用decoder模型。

但是在训练过程中，模型存在encoder部分，也存在训练的输入数据，并且整个模型是一起训练的。模型训练时，对于decoder模型来说，隐变量的噪声自然是越小越好，也就是希望隐变量方差为0，那岂不是变成了AE么？这时候加入的latent loss就发挥了作用，kl散度保证encoder拟合的分布接近标准正态分布，方差尽可能接近1，因此这个情况是encoder不希望发生的。

可以看到VAE存在一些trade-off，从正则的角度更好理解。encoder希望输出的分布接近标准正态分布的特性，而decoder希望分布的噪声小，尽量确定。

总结来说，VAE是隐变量生成模型，希望直接从隐变量能生成所有可能的数据。为了衡量数据生成的好坏，增加encoder对后验分布$p(z|x_i)$的拟合找到分布对应关系。

推导和补充

其实图2的模型画的不是很标准，毕竟不是真的一下子训练出那么多的正态分布用于decoder。我的理解是decoder对于每一个从隐变量采样出的生成数据，可以找到对应的训练数据。而这个过程中$\mathbf{x}_1$ $\mathbf{x}_2$ …$\mathbf{x}_N$可以是逐个迭代的，也可以是以batch形式迭代的。代码中可以很好的体现迭代过程，那么数学上如何体现呢？

公式（1）推导

Pytorch代码片段

以下是VAE生成是个的代码片段。embedding部分其实可以忽略，为了复现论文Generating Sentences from a Continuous Space
完整代码见 DemoML/VAE_NLG/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class VAE(nn.Module):
    def __init__(self, args):
        super().__init__()
        self.embed = nn.Embedding(self.vocab_size, self.embed_dim)
        self.encode = Encoder(self.embed_dim,
                              self.enc_hsz, self.enc_layers, self.dropout)

        self._enc_mu = nn.Linear(self.enc_hsz * 2, self.latent_dim)#生成均值的神经网络
        self._enc_log_sigma = nn.Linear(self.enc_hsz * 2, self.latent_dim)#生成对数方差的神经网络

        self.decode = Decoder(self.embed_dim, self.latent_dim,
                              self.dec_hsz, self.dec_layers, self.dropout, self.vocab_size)

    def forward(self, enc_input, dec_input, input_lengths, enc_hidden=None, dec_hidden=None):
        enc_ = self.embed(enc_input)#encoder输入文本embedding
        enc_output, enc_hidden = self.encode(enc_, input_lengths) #encoding过程
        z = self._gaussian(enc_output) #采样后验分布
        dec_ = self.embed(dec_input) #decoder输入文本embedding
        dec, dec_hidden = self.decode(dec_, z) #把采样的z输入decoder
        return dec, self.latent_loss, enc_hidden, dec_hidden

    def _gaussian(self, enc_output):
        def latent_loss(mu, sigma):
            pow_mu = mu * mu
            pow_sigma = sigma * sigma
            return 0.5 * torch.sum(pow_mu + pow_sigma - torch.log(pow_sigma) - 1, dim=-1).mean()
        mu = self._enc_mu(enc_output) #生成均值
        sigma = torch.exp(self._enc_log_sigma(enc_output))#生成方差
        self.latent_loss = latent_loss(mu, sigma)#计算latent loss kl(q(z)|p(z|x))

        std_z = torch.normal(0,1,size=sigma.size()) #\epsilon 符合标准正态分布的噪声
 
        return mu + sigma * std_z #返回后验采样

生成过程直接利用标准正态分布$p(z)$采样，通过decoder生成数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def generate_songci(model, args, max_len=30):

    z = torch.normal(0,1,size=(1,args.latent_dim))#从标准正态分布p(z)采样
    next_word = torch.ones(1, 1, device=device, dtype=torch.long) * BOS
    
    portry = ""
    length = 0
    hidden = None

    while True:
        input_sent = next_word.expand(1,1).to(device)
        encode = model.embed(input_sent)#embedding
        output, hidden = model.decode(encode, z, hidden)#利用decoder生成数据
        prob = output.squeeze().data

        score, next_word = torch.max(prob[igore_idx-1:],dim=-1)
        word = args.idx2word[next_word.item()+ igore_idx-1]

        if word == WORD[EOS] or length == max_len-1:
            portry += "。"
            break
        else:
            portry += word
            length += 1

    return portry[:-1] + "。"