学习和推断的时候通常会包含难解积分(intractable integral),可以使用samlping去估计这些积分项。
主要介绍蒙特卡洛积分,使用均值估计期望的原理及存在问题,如何使用重要采样获得一般化的期望,列举其他的采样方法。
前言
做学习和推断的时候通常会包含难解积分(intractable integral),比如:
- 边缘化(maginalisation):
- 对函数给定$g$,求期望(Expectations) :
隐变量模型的似然函数(likelihood) 和 对数似然函数梯度(gradient of the log likelihood)
未归一化模型有难解配分函数(intractable partition funtions)
存在同时含有隐变量和未归一化的模型(如 受限玻尔兹曼机 Restricted Boltzmann Machine)
- 对于难解积分有时可以通过使用其他学习准则避免,例如score matching(不match log likelihood,而是match 导数,用来避免计算归一化项)
- 这里我们使用samlping去估计这些积分
正文
蒙特卡洛积分 Monte Carlo integration
蒙特卡洛积分:通过计算样本均值估计积分
- 均值估计期望(Approximating expectations by averages)
- 重要采样(Importance sampling)
均值估计期望(Approximating expectations by averages)
- 独立同分布样本(iid data: independent and indentically distributed data)的均值:假设$x_i$是$x \sim p(x)$的iid观测值,有
- 样本均值是无偏的
- 变异性 (Variability)
- 考虑更一般化的积分
其中 $\mathbf x_i \sim p(\mathbf x)$。
如果$\mathbf x_i$是独立同分布样本,估计方差为$\frac{1}{n} \mathbb{V}[g(\mathbf x_i)]$
例子
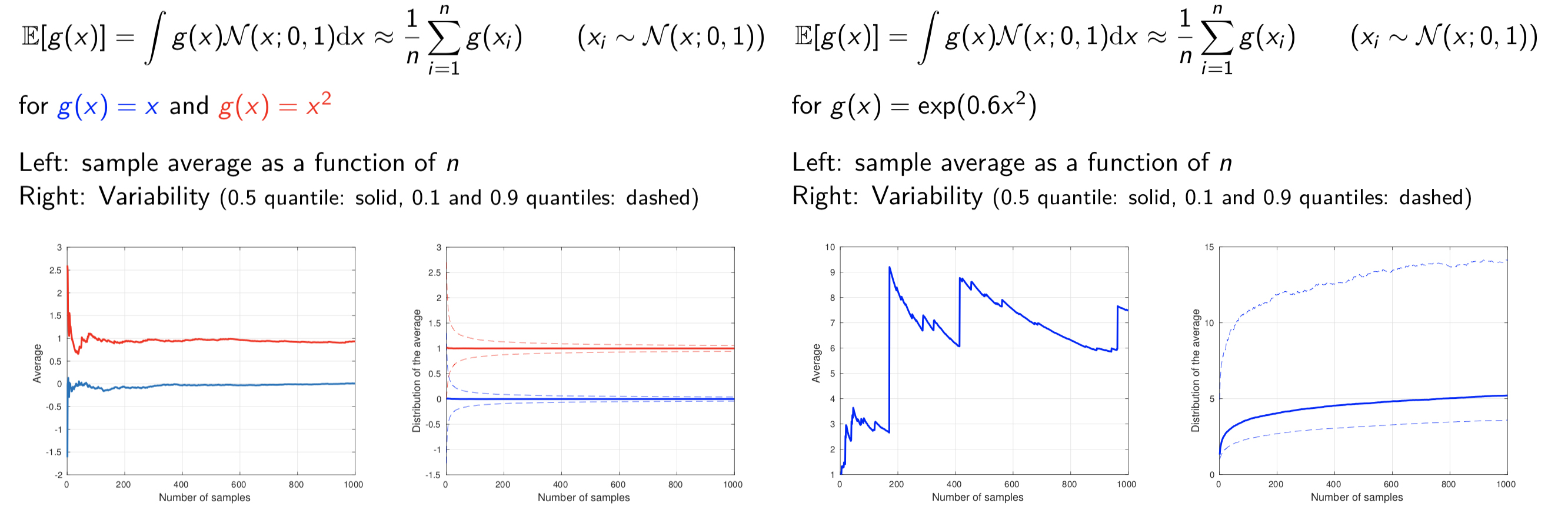
分析:
- 右图中存在明显的错误:当样本增加的时候,均值依然在抖动
- 非常大的不衰减变异
- 注意到积分并不是有限的,但是对于给定$n$,样本均值是有限的。所以估计方法需要改进
- 使用样本均值估计之前,一定要检查变异值
重要采样(Importance sampling)
基本想法:如果需要计算的积分和期望并不成对应关系,我们可以利用概率密度函数(pdf) $q$,将积分写成针对$q$的期望
其中 $\mathbf x_i \sim q(\mathbf x)$ (iid) $q$是重要分布(importance distribution or proposal distribution)
- 由于方差问题(待编辑),优化$q$为
这个优化$q$并不能计算出来,但是给予我们选择$q(\mathbf x)$ 的指导:
- 当$g(\mathbf x)$较大时,$q(\mathbf x)$也应该较大
- $|g(\mathbf x)|/q(\mathbf x)$的比值约为常数
使用重要采样计算期望
目标:使用样本均值估计 $\mathbb E _ {p(\mathbf x)}(g(\mathbf x))$,但从分布$p(\mathbf x)$采样较为困难
$w_i =\frac{p(\mathbf x_i)}{q(\mathbf x_i)}$称为重要权重(importance weights) 对于没有归一化的分布$\tilde p(\mathbf x)$
归一重要权重(normalised importance weights)为$\frac{w_i}{\sum_{i=1}^n w_i}$
其他采样方法 Samlping
比较常见,有大量介绍性文章,不做展开
- 简单单变量采样 (Univariate sampling)
- 离散随机变量的采样
- 连续随机变量的采样:Inverse Sampling
- 拒绝采样 (Rejection sampling)
- 多重变量采样(Sampling from high-dimensinal multivatiate distribution)
- 祖先采样,原始采样 (Ancestral sampling)
- 吉布斯采样 (Gibbs sampling)
小结与理解
- closed form solution: 对于所求目标函数给出一个数学表达式 $f(x) = ax+b$
- exact inference: 对给定的$x$,可以给出 $f(x)$的值,相当于知道怎么做这个映射,但并不一定有确切数学表达。比较典型的有 message-passing, sum-product.
- analytical solution: …exact inference 也可以有analytical solution
- approximatation: 一般没有closed form solution,也无法使用exact inference的时候可以用近似方法,比如 Monte Carlo Integral.
- 对于intractable的问题,可以转换成推断问题(inference)的形式,或者转换成可以用approximatation解决的形式