基于模型学习的基本概念 Basics of Model-based Learning

本文主要内容：如何从观测样本学习模型（参数）/分布

理解观测数据，样本，未知分布之间的关系。
三种模型(Model)概念和实例：概率模型(Probabilistic model)，统计模型(Statistical Model)和贝叶斯模型(Bayesian Model)。
两种学习方法的概念，区别和实例：最大似然估计(MLE, Maximum Likelihood estimation)和贝叶斯推断(Bayesian inference)

前言

对于分布 $p(\mathbf x \mid \mathbf y_0) = \frac{\sum_{\mathbf z} p(\mathbf x,\mathbf y,\mathbf z)}{\sum_{\mathbf x,\mathbf z} p(\mathbf x,\mathbf y,\mathbf z}$

假设所有变量$\mathbf x, \mathbf y, \mathbf z$ 维度是$d = 500$，向量中的每一个元素有$K=10$种取值。

情况1

问题：确定分布 $p(\mathbf x, \mathbf y, \mathbf z)$，需要$K^{3d}-1 = 10^{15000}-1$非负数值（参数）。这几乎是不可能的
论题： Representaion 利用弱假设更有效得表达分布$p(\mathbf x, \mathbf y, \mathbf z)$
有向图模型(DGM, directed graphical models),无向图模型(UGM, undirected graphical models),因子图(FG, factor graphs)
因子分解和（变量间的）独立(Factorisation and indenpendencies)

情况2

问题：为了计算分子求和表达式，需要顺序遍历$K^d = 10^{500}$非负数；计算分母求和表达式，需要顺序遍历$K^{2d}=10^{10000}$非负数。计算不可能。
论题：Exact inference 继续利用以上弱假设，高效计算后验概率 Posterior probability（针对归一化模型）或者求取数值（未归一化模型）。
再次利用因子分解（factorisation），分配律（distributive law）和缓存计算（caching computations）：
- 缓存计算（caching computations：由于因子分解使分子和分母的求和表达式计算时，出现了大量相同的计算量，因此减少了重复计算
例如：消元法 (Variable elimination)，Sum/Max-product message passing
实例：隐藏马尔可夫模型的推断（inference for hidden Markov models）

情况3（本文涉及）

问题：如何得到 $p(\mathbf x, \mathbf y, \mathbf z)$ 中的这些非负数？
论题：Learning 如何从（观测）数据中学习这些数值（参数）？

基本概念：数据与分布

观测数据，样本，未知数据的分布

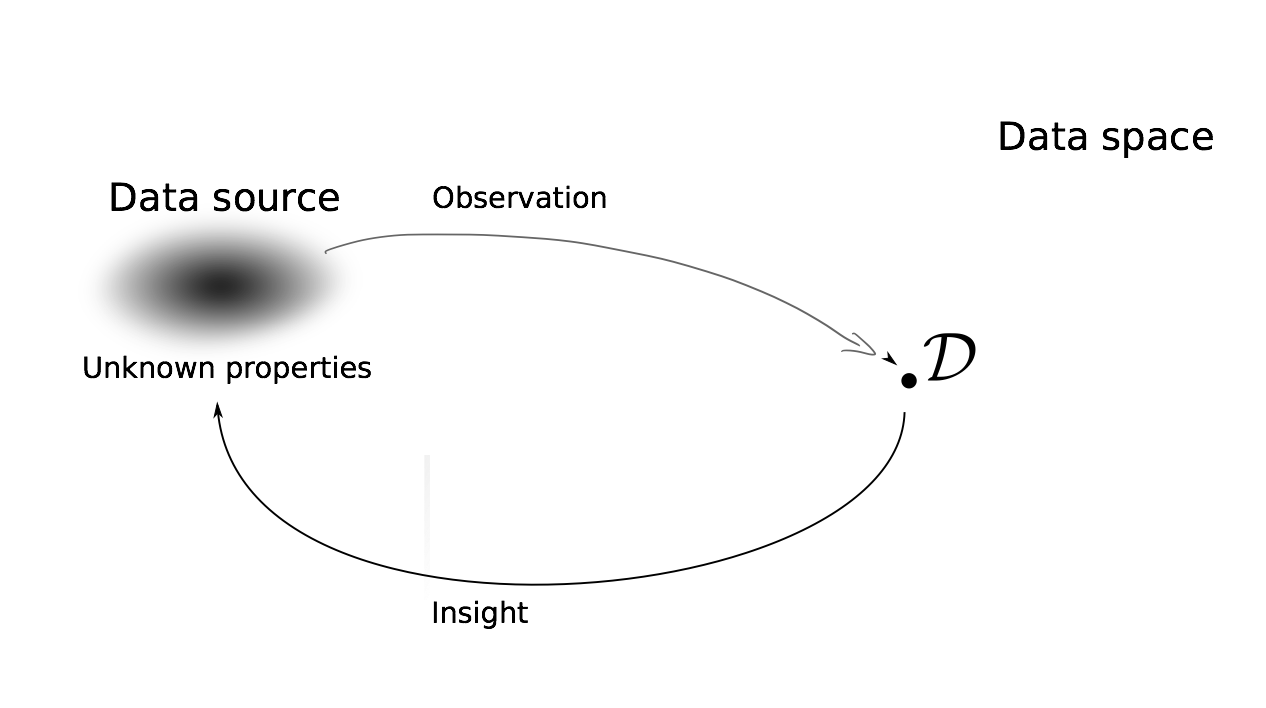
任务：利用观测数据$\mathcal D$学习数据源特征（分布），由此可以进一步做 概率推断，决策
一般来说，假设观测数据$\mathcal D$是从一个未知分布$p_*(\mathcal D)$随机采样的数据。换句话说，我们考虑数据$\mathcal D$是分布$p_*$的随机变量的观测值。 $\mathcal D \sim p_\*(\mathcal D)$
例子：用隐藏马尔可夫模型（HMM）中的trasition 和 emission 分布，利用祖先采样/原始采样(ancestral sampling)生成数据。因此，我们得到了可见量(visibles) $(v_1,v_2,v_3,\cdots,v_T) \sim p(v_q,\cdots,v_t)$

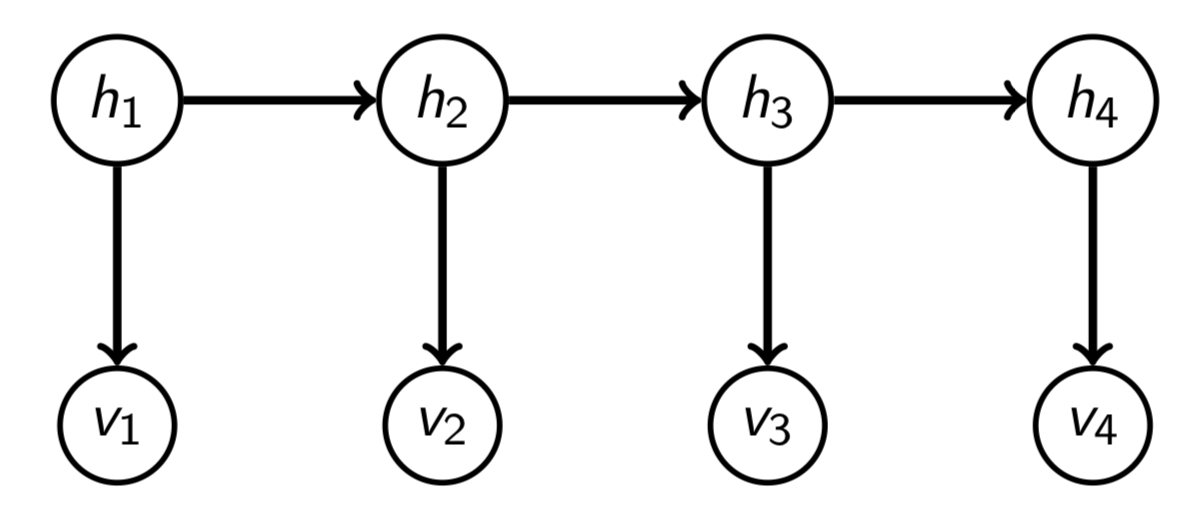
然后呢，你把这些可见量给你的朋友，他/她并不知道你用来产生数据的分布，在这个例子中就是trasition 和 emission 分布，也可能不知道你用的是隐藏马尔可夫模型(HMM)，所以对于你朋友来说: $\mathcal D = (v_1,v_2,v_3,\cdots,v_T) \quad \quad \mathcal{D} \sim p_\*(\mathcal D)$

独立同分布数据(Independent and indentically distributed (iid) data)

假设数据$\mathcal D = \{\mathbf x_1,\cdots, \mathbf x_n\}$ 有 $p_\*(\mathcal D) = \prod \limits _{i=1}^n p_\*(\mathbf{x}_i)$ 那么这组数据（或者说数据对应的随机变量）是独立同分布的（iid）。$\mathcal D$ 也被称作是分布$p_*$的一个随机采样。换句话说，每一个数据点$\mathbf x_i$是从同一个分布$p_*$中独立得到的。
例子1：还是刚才HMM的例子，$n$个数据点，每一个数据点都包括$(v_1,v_2,v_3,\cdots,v_T)$，这$n$个数据都是独立从相同的trasition 和 emission 分布产生的。
例子2：对于分布
$p(x_1,x_2,x_3,x_4,x_5) = p(x_1)p(x_2)p(x_3 \mid x_1.x_2)p(x_4 \mid x_3)p(x_5\mid x_2)$
我们知道这些条件概率，可以进行祖先/原始采样（ancestral sampling），并且采样$n$次。

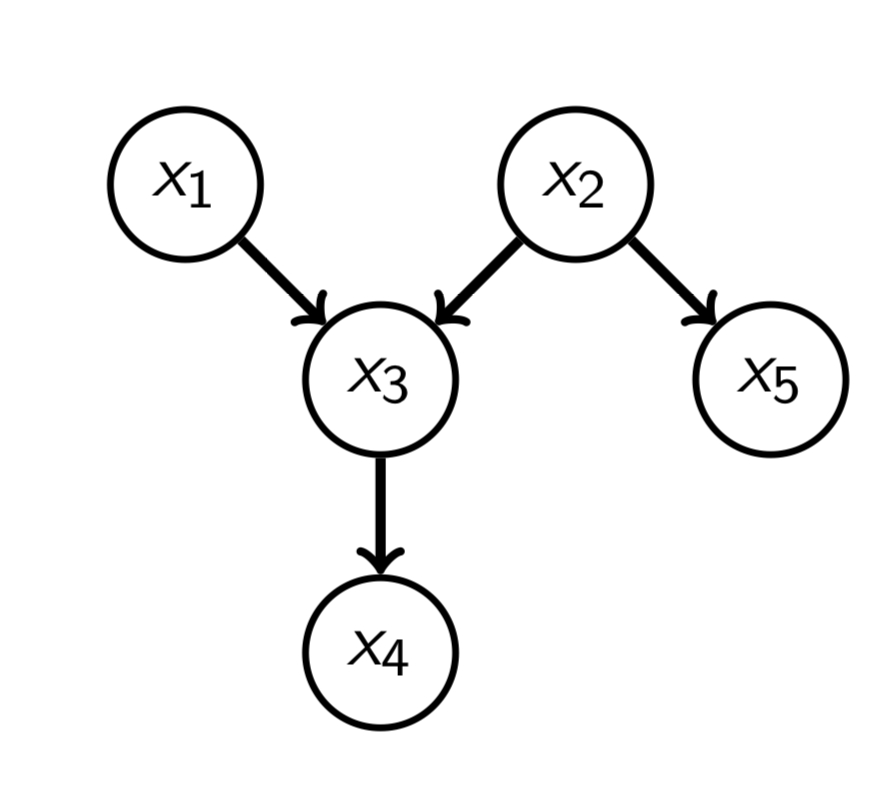
记录$n$次观测值$x_4$：$x_4^{(1)},x_4^{(2)},\cdots,x_4^{(n)}$，并把这些观测值给你的朋友，她/他并不知道你是如何产生这些数据的，但知道这些数据是独立同分布的(iid)。

因此对于你的朋友，每一个$x_4^{(i)}$ 都是$x_i \sim p_*$ 的数据点。

基本概念：模型

利用模型（Model）学习数据

建立含有隐藏特征$\mathbf {\theta}$的模型，这里的$\mathbf {\theta}$也称为参数
寻找符合观测数据$\mathcal D$的$\mathbf {\theta}$
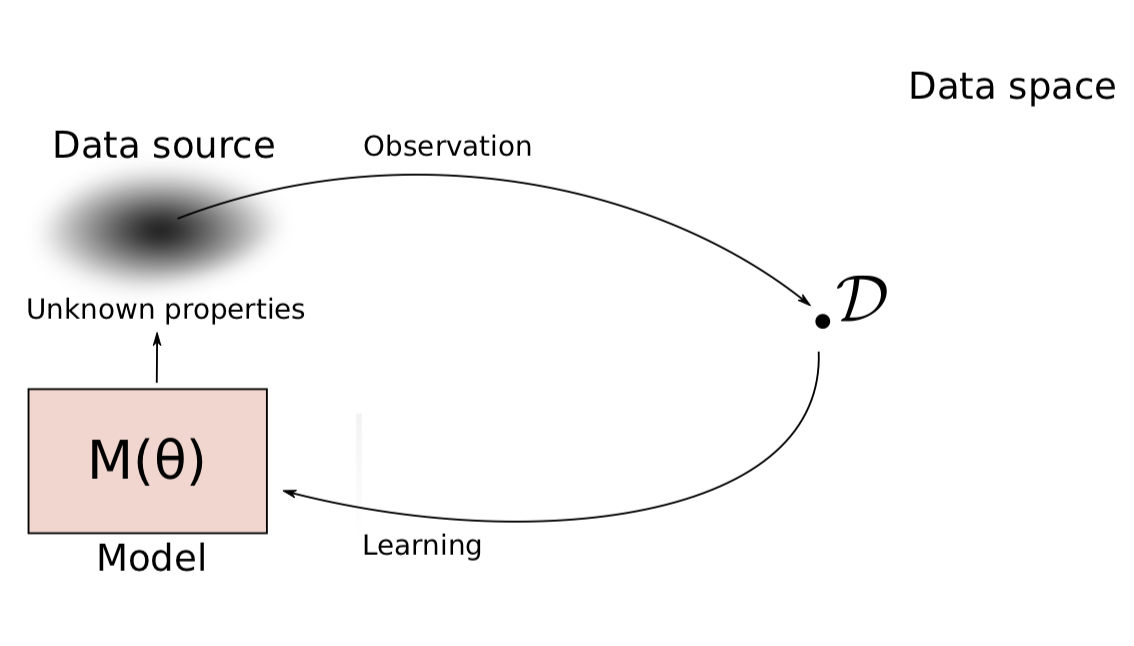
注意这里模型（Model）有多种指向，本文考虑三种模型
- 概率模型(Probabilistic model)
- 统计模型(Statistical model)
- 贝叶斯模型(Bayesian model)
名称在文章中可能有混用，比如直接称概率模型或者统计模型为模型。

概率模型

运用概率理论，将不确定事件的可能性数据化(quantify)，是一种对现实的抽象表达。技术上说,概率模型恒等于概率分布（概率质量函数/概率密度函数：Probabilistic model $\equiv$ probability distribution (pmf/pdf)
概率模型由概率$Pr$表达。使用概率质量函数（pmf）表达，则 $\begin{eqnarray} p_x(1)&=&0.11 \quad &or& \quad p(x=1)&=&0.11\\ p_{y|x}(1\mid1)&=&0.8 \quad &or& \quad p(y=1 \mid x=1)&=&0.8\\ p_{y|x}(0\mid0)&=&0.95 \quad &or& \quad p(y=0 \mid x=0)&=&0.95 \end{eqnarray}$ *这里描述概率的记号$Pr$和$p$有混用

统计模型

用参数替换上述概率模型的具体数字，我们就能得到（参数化）的统计模型
$\begin{eqnarray} p_x(1)&=&\theta_1\\ p_{y|x}(1\mid1)&=&\theta_2\\ p_{y|x}(0\mid0)&=&\theta_3 \end{eqnarray}$
对于每一个$\theta_i$的值，符合不同的概率质量函数（pmf），概率质量函数(pmf)和参数之间的依存关系如下表示：
$\begin{eqnarray} p(x=1; \theta_1)&=&\theta_1\\ p(y=1 \mid x=1; \theta_2)&=&\theta_2\\ p(y=0 \mid x=0; \theta_3)&=&\theta_3 \end{eqnarray}$
或者可以表达为$p(x,y;\mathbf {\theta})$，其中 $\mathbf {\theta} = (\theta_1, \theta_2, \theta_3)$ 是参数向量
统计模型对应一系列通过参数索引的概率模型（indexed by the parameters): $\{p(\mathbf{x};\mathbf{\theta})\}_{\mathbf{\theta}}$

贝叶斯模型

贝叶斯模型，可以理解为给统计模型的参数$\mathbf {\theta})$设置先验概率分布(prior probability distribution)。
每一个 $\{p(\mathbf{x};\mathbf{\theta})\}_{\mathbf{\theta}}$ 中的成员，是在参数$\mathbf {\theta})$下，变量$\mathbf x$的pmf/pdf。使用$p(\mathbf x \mid \mathbf \theta)$ 表示这个条件概率分布pmf/pdf。
条件分布$p(\mathbf x \mid \mathbf \theta)$ 和先验分布 $p(\theta)$可以定义联合分布：$p(\mathbf x, \mathbf \theta)=p(\mathbf x \mid \mathbf \theta)p(\mathbf \theta)$
含有变量 $\mathbf x$ 的贝叶斯模型 $=$ 含有变量$(\mathbf x, \mathbf \theta)$的概率模型
先验可以被参数化，比如$p(\mathbf \theta;\mathbf \alpha)$。参数$\mathbf \alpha$是超参数。

将图模型表达为统计模型

有向图模型和无向图模型都是一系列概率分布。例如所有的概率分布$p$都可以因子分解为 $p(\mathbf x) = \prod \limits_i p(x_i|pa_i) \quad or \quad p(\mathbf x) \propto \prod \limits_i \phi_i(\mathcal X_i)$ 因此他们都是统计模型
$p(x_i|pa_i)$和$\phi_i(\mathcal X_i)$的参数族，就对应参数化统计模型
$p(\mathbf x;\mathbf \theta) = \prod \limits_i p(x_i|pa_i;\mathbf \theta) \quad or \quad p(\mathbf x;\mathbf \theta) \propto \prod \limits_i \phi_i(\mathcal X_i;\mathbf \theta)$
其中 $\mathbf \theta = (\mathbf \theta_1,\mathbf \theta_1,\cdots)$。

例子：癌症-石棉-吸烟 (cancer-asbestos-smoking)

见附件

基本概念：分割函数与未归一化统计模型

分割函数(partition function)

概率密度函数和概率质量函数的和为 $1$（定义）
但是对于参数化吉布斯分布(parametrised Gibbs distributions) $p(\mathbf x;\mathbf \theta) \propto \prod \limits_i \phi_i(\mathcal X_i;\mathbf \theta)$ 并无法保证积分/总和为 $1$。
为了概率归一化，使用分割函数$Z(\mathbf \theta)$把未归一化模型$\tilde p(\mathbf x;\mathbf \theta) \propto \prod _i \phi_i(\mathcal X_i;\mathbf \theta)$分割为 $Z(\mathbf \theta) = \int \tilde p(\mathbf x;\mathbf \theta) d \mathbf x \quad or \quad Z(\mathbf \theta) = \sum \limits_{\mathbf x} \tilde p(\mathbf x;\mathbf \theta)$
通过设置 $p(\mathbf x;\mathbf \theta) = \frac{\tilde p(\mathbf x;\mathbf \theta)}{Z(\mathbf \theta) }$ 对于所有参数$\mathbf \theta$，概率总和/积分为$1$

未归一化统计模型

对于每一个$\{p(\mathbf{x};\mathbf{\theta})\}_{\mathbf{\theta}}$中的元素，都能保证总和/积分为$1$。也就是说，对于所有$\mathbf \theta$ $\int p(\mathbf x;\mathbf \theta) d \mathbf x = 1 \quad or \quad \sum \limits_{\mathbf x} p(\mathbf x;\mathbf \theta) = 1$ 则称这个统计模型是归一化的。否则，这个统计模型是未归一化的。
一般来说无向图模型是未归一化的，但是可以通过设置分割函数进行归一化处理。
注意，分割函数可能很难计算，这会导致使用likelihood-based学习时碰到问题。

从归一化模型中读取分割函数

考虑未归一化高斯模型$\tilde p(\mathbf x;\mathbf \theta) = \exp(-\frac{1}{2} \mathbf {x}^T\mathbf \Sigma ^{-1} \mathbf {x})$，其中$\mathbf x \in \mathbb R^m$并且$\mathbf \Sigma$ 是对称矩阵。
参数$\mathbf \theta$是包括对角线在内的$\mathbf \Sigma$的下三角矩阵（或上三角矩阵）。
分割函数有闭式解(cloed form) $Z(\mathbf \theta) = |\det 2 \pi \mathbf \Sigma|^{1/2} \quad \quad p(\mathbf x;\mathbf \theta) = \frac{1}{|\det 2 \pi \mathbf \Sigma|^{1/2}} \exp(-\frac{1}{2} \mathbf {x}^T\mathbf \Sigma ^{-1} \mathbf {x})$
这同时也说明，我们可以通过反向该过程，从归一化模型$p(\mathbf x;\mathbf \theta)$中读取分割函数，只要分割函数中不存在变量 $\mathbf x$。例如 $p(\mathbf x;\mathbf \theta) \rightarrow p(\mathbf x;\mathbf \theta) = \frac{\tilde p(\mathbf x;\mathbf \theta)}{Z(\mathbf \theta) }$ 将分割归一化模型$p(\mathbf x;\mathbf \theta)$ 未归一化模型。

应用范围限制(The domain matters)

孤岛模型，玻耳兹曼机：$\tilde p(\mathbf x;\mathbf \theta) = \exp(-\frac{1}{2} \mathbf {x}^T\mathbf A \mathbf {x})$，其中$\mathbf x \in \mathbb \{0,1\}^m$，并且$\mathbf A$ 是对称矩阵。参数$\mathbf \theta$是包括对角线在内的$\mathbf \Sigma$的下三角矩阵（或上三角矩阵）。
和上一小节的区别
- 标记和参数： $\mathbf A$ 和 $\mathbf \Sigma ^{-1}$没有影响
- 但是，$\mathbf x \in \mathbb \{0,1\}^m$和$\mathbf x \in \mathbb R^m$对求解有影响
通过求和（而不是积分）定义分割函数 $Z(\mathbf \theta) = \sum \limits_ {\mathbf x \in \mathbb \{0,1\}^m} \exp(-\frac{1}{2} \mathbf {x}^T\mathbf A \mathbf {x})$
不存在$Z(\mathbf \theta)$的解析解。当$m$很大时，计算量非常大。

基本概念：什么是学习？

统计模型的学习 —— 参数估计

利用数据从一些列概率模型 $\{p(\mathbf{x};\mathbf{\theta})\}_{\mathbf{\theta}}$ 中选一个$p(\mathbf{x};\mathbf{\hat \theta})$: $\{p(\mathbf{x};\mathbf{\theta})\}_{\mathbf{\theta}} \overset{data \mathcal D}{\rightarrow} p(\mathbf{x};\mathbf{\hat \theta})$
换句话说就是，利用数据，从一堆可能的参数$\mathbf{\theta}$中，选择估计值$\mathbf{\hat \theta}$。

贝叶斯模型的学习 —— 贝叶斯推断

利用数据，确定所每一个可能的参数$\mathbf{\theta}$的合理性，这个合理性通过后验 pdf/pmf 表达。贝叶斯推断并不是从一堆可能的参数$\mathbf{\theta}$中选择一个，而是评估每一个可能的参数$\mathbf{\theta}$。因此，学习贝叶斯模型是一个推断问题，是生成数据的逆向过程，有向图模型如下：

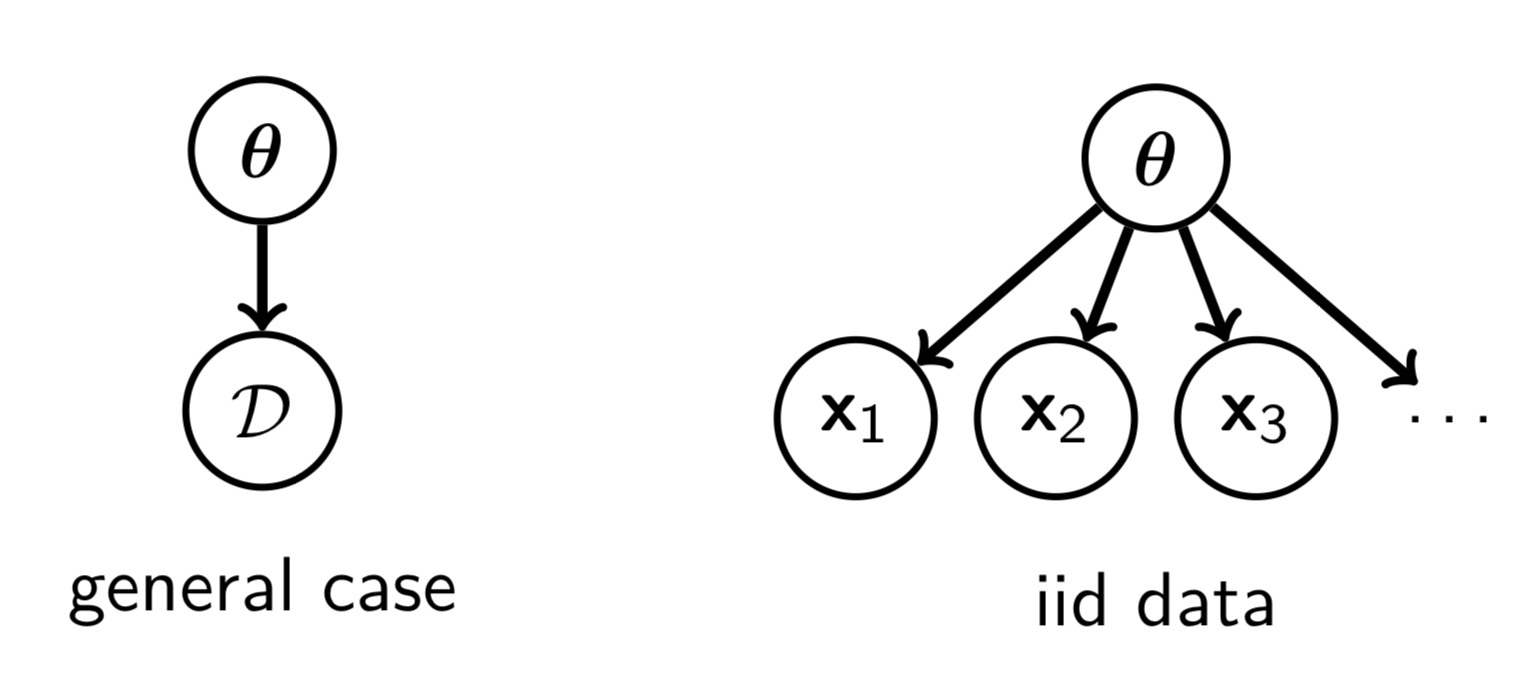
给予数据$\mathcal D$，我们需要预测下一个数据$\mathbf x$的值。如果我们通过参数估计的方法，预测分布为$p(\mathbf{x};\mathbf{\hat \theta})$。在贝叶斯推断中，我们进行以下计算

$p(\mathbf x \mid \mathcal D) = \int p(\mathbf x, \mathbf \theta \mid \mathcal D)d \mathbf{\theta} = \int p(\mathbf x \mid \mathbf \theta, \mathcal D)p(\mathbf \theta \mid \mathcal D) \quad \overset{\mathrm{if}\ \mathbf x \perp\mspace{-10mu}\perp \mathcal D \mid \mathbf \theta}{=} \quad \int p(\mathbf x \mid \mathbf \theta)p(\mathbf \theta, \mathcal D)$

这个过程可以理解为使用权重 $p(\mathbf \theta, \mathcal D)$平均预测$p(\mathbf x \mid \mathbf \theta)$。

有向图模型表达预测分布

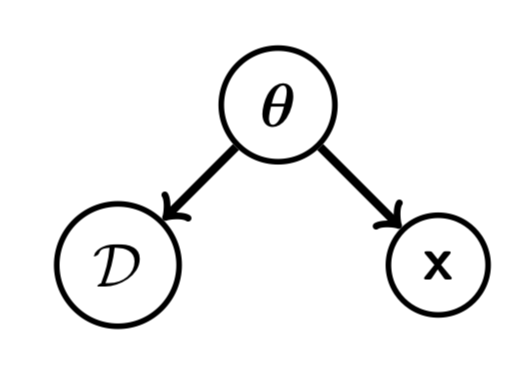
参数估计的方法

参数估计的方法有很多，大多数都对应解决一个优化问题。比如，对于目标函数$J$，解决$\mathbf {\hat \theta} = \mathrm{argmax}_{\mathbf \theta} J(\mathbf \theta, \mathcal D)$。这个过程叫M-estimation。这其中

最大似然估计（maximum likelihood estimation, MLE）有着广泛的运用。
Moment matching：寻找一个参数设置，使得我们估计的模型给予的moment和从数据重计算得到的moment一致。观测数据的moment也称为empirical moments。
最大后验估计：寻找$\mathbf \theta$最大化后验值$\mathbf {\hat \theta} = \mathrm{argmax}_{\mathbf \theta}(\mathbf \theta|\mathcal D)$，得到的参数设置就是估计参数$\mathbf \theta$。
Score maching 也是一种参数估计方法，尤其对于未归一化模型（吉布斯分布, Gibbs distribution）有着很好的特性。

学习：最大似然估计

似然函数 $L(\mathbf \theta)$

似然函数测量参数$\mathbf \theta$和观测数据$\mathcal D$一致性。换句话说，似然函数给出采样$\mathbf \theta$所确定的模型得到的数据和观测数据$\mathcal D$一致的可能性。离散随机变量，计算数据匹配(exace match)；对于连续随机变量，计算小邻域。数学上，对于似然函数的定义为

$L(\mathbf \theta) = p(\mathcal D; \mathbf \theta)$

其中 $p(\mathcal D; \mathbf \theta)$ 是参数化模型的概率密度函数/概率质量函数(pdf/pmf)。

似然函数暗示了参数值的似然（可能性），未不是数据的可能性。
对于iid 数据(独立同分布数据) $\mathbf x_i, \cdots, \mathbf x_n$ $L(\mathbf \theta) = \prod \limits _{i=1}^n p(\mathbf x_i;\mathbf \theta)$
对数似然函数$\ell (\mathbf \theta) = \log L(\mathbf \theta)$, 对于iid 数据。 $\ell(\mathbf \theta) = \sum \limits_ {i=1}^n \log p(\mathbf x_i;\mathbf \theta)$

最大似然估计

最大似然估计的数学表达为

$\mathbf{\hat \theta} = \mathrm{argmax}_{\mathbf \theta} \ell (\mathbf \theta) = \mathrm{argmax}_{\mathbf \theta} L (\mathbf \theta)$

解决这个优化问题需要数值法计算，并且我们只能找到局部最优解（即便是次优解也相当有用）。在一些比较简单的情况下，闭式解是可能的。

最大似然估计例子：高斯，伯努利和所有随机变量可见并为离散值的有向图模型

正文中只列举结论，具体步骤见附件

高斯分布的极最大似然估计为 $\hat \mu = \frac{1}{n}\sum \limits _{i=1}^n x_i \quad \quad \hat \sigma ^2 = \frac{1}{n} \sum \limits _{i=1}^n(x_i-\hat \mu)^2$ 其中$\hat \mu$和$\hat \sigma ^2$分别为高斯分布的参数——均值和方差的估计值，$n$为样本空间，$x_i$为某一个样本。
伯努利分布的最大似然估计为
$\hat \theta = \frac{n_{x=1}}{n}$
其中$\hat \theta$是伯努利分布参数($Pr(x = 1)= \theta$)的估计值,$n_{x=1}$是样本中$x=1$的样本数，$n$为样本空间。

因此，伯努利分布参数的最大似然估计值就是，观测样本中为1的样本的比例。
所有随机变量可见并为离散值的有向图模型——癌症-石棉-吸烟 (cancer-asbestos-smoking)

随机变量 $a$, $s$是伯努利分布，同上计算，对于条件概率$p(c|a,s)$的参数
$\hat p (c =1 \mid a=0, s = 0) = \hat \theta_c^1 = \frac{\sum_{i=1}^n \mathbb{I} (c_i = 1, a_i = 0, s_i = 0)}{\sum_{i=1}^n \mathbb {I} (a_i = 0, s_i = 0)}$
$\mathbb{I}(\cdot)$是指示函数。

最大似然估计是moment maching的一种形式

$\mathbf \theta$ 的似然:指从$\mathbf \theta$决定的模型采样获得的数据与观测数据$\mathcal D$之间的的相似的概率
最大似然估计(MLE)：得到的参数设置，使得模型生成$\mathcal D$的概率值最大。
从另外一个角度看：在某一个模型下的参数设置计算的moments和观测数据的empirical moments一致
数学解释：
$p(\mathbf x;\mathbf \theta)=\frac{\tilde p (\mathbf x;\mathbf \theta)}{Z(\mathbf \theta)}$
MLE的$\hat{\mathbf \theta}$满足:
$\int \mathbf m (\mathbf x;\hat{\mathbf \theta}) p (\mathbf x;\hat{\mathbf \theta}) d \mathbf x = \frac{1}{n}\sum \limits _{i=1}^n \mathbf m (\mathbf x_i;\hat{\mathbf \theta})$
其中 “moments” $\mathbf m (\mathbf x;{\mathbf \theta})$是
$\mathbf m (\mathbf x;{\mathbf \theta}) = \nabla_{\mathbf \theta} \log \tilde p (\mathbf x;\mathbf \theta)$
证明
MLE的必要条件是满足：$\nabla_{\mathbf \theta}\ell(\mathbf \theta)|_{\hat {\mathbf \theta}}$
将对数似然函数的梯度写作：
$\begin{eqnarray} \nabla_{\mathbf \theta}\ell(\mathbf \theta) &=& \nabla_{\mathbf \theta} \sum \limits _{i=1}^n\log p(\mathbf x_i;\mathbf \theta) = \nabla_{\mathbf \theta} \sum \limits _{i=1}^n\log \frac{\tilde p (\mathbf x_i;\mathbf \theta)}{Z(\mathbf \theta)}\\ &=& \nabla_{\mathbf \theta} \sum \limits _{i=1}^n\log \tilde p (\mathbf x_i;\mathbf \theta) - \nabla_{\mathbf \theta}\log n Z(\mathbf \theta)\\ &=& \sum \limits _{i=1}^n \nabla_{\mathbf \theta} \log \tilde p (\mathbf x_i;\mathbf \theta) - n \nabla_{\mathbf \theta} \log Z(\mathbf \theta)\\ &=& \sum \limits _{i=1}^n \mathbf m(\mathbf x_i;\mathbf \theta) - n \nabla_{\mathbf \theta} \log Z(\mathbf \theta) \end{eqnarray}$
其中梯度$\nabla_{\mathbf \theta} \log Z(\mathbf \theta)$为:
$\begin{eqnarray} \nabla_{\mathbf \theta} \log Z(\mathbf \theta) = \frac{1}{Z(\mathbf \theta)}\nabla_{\mathbf \theta}Z(\mathbf \theta) = \frac{1}{Z(\mathbf \theta)} \nabla_{\mathbf \theta} \int \tilde p (\mathbf x;\mathbf \theta) d \mathbf x = \frac{ \int \nabla_{\mathbf \theta} \tilde p (\mathbf x;\mathbf \theta) d \mathbf x}{Z(\mathbf \theta) } \end{eqnarray}$
由于$(\log f (x))’ = \frac{f’(x)}{f(x)}$，得出$f’(x) = (\log f (x))’ f(x)$, 可以将上式写作：

$\begin{eqnarray} \nabla_{\mathbf \theta} \log Z(\mathbf \theta) &=& \frac{ \int \nabla_{\mathbf \theta} [\log \tilde p (\mathbf x;\mathbf \theta)] \tilde p (\mathbf x;\mathbf \theta) d \mathbf x}{Z(\mathbf \theta) } \\ &=& \int \nabla_{\mathbf \theta} [\log \tilde p (\mathbf x;\mathbf \theta)] p (\mathbf x;\mathbf \theta) d \mathbf x\\ &=& \int \mathbf m (\mathbf x;{\mathbf \theta}) p (\mathbf x;{\mathbf \theta}) d \mathbf x \end{eqnarray}$

因此对数似然函数$\ell(\mathbf \theta)$的梯度:

$\begin{eqnarray} \nabla_{\mathbf \theta}\ell(\mathbf \theta) = \sum \limits _{i=1}^n \mathbf m(\mathbf x_i;\mathbf \theta) - n \int \mathbf m (\mathbf x;{\mathbf \theta}) p (\mathbf x;{\mathbf \theta}) d \mathbf x \end{eqnarray}$

根据必要条件: MLE的参数$\hat{\mathbf \theta}$使得梯度为0，得到结果

$\begin{eqnarray} \sum \limits _{i=1}^n \mathbf m(\mathbf x_i; \hat{\mathbf \theta}) - n \int \mathbf m (\mathbf x;\hat {\mathbf \theta}) p (\mathbf x;\hat {\mathbf \theta}) d \mathbf x = 0 \end{eqnarray}$

推出

$\int \mathbf m (\mathbf x;\hat{\mathbf \theta}) p (\mathbf x;\hat{\mathbf \theta}) d \mathbf x = \frac{1}{n}\sum \limits _{i=1}^n \mathbf m (\mathbf x_i;\hat{\mathbf \theta})$

如何评价和理解最大似然估计？

最大似然估计忽略了数据中存在的信息

例如：伯努利模型的观测数据$\mathcal D = （0，0，0，0，0，0，0，1，1，1，\cdots）$的参数值为$\frac{1}{3}$似然函数为
图(a),(b),(c)分别为2，5，10个观测数据时的似然函数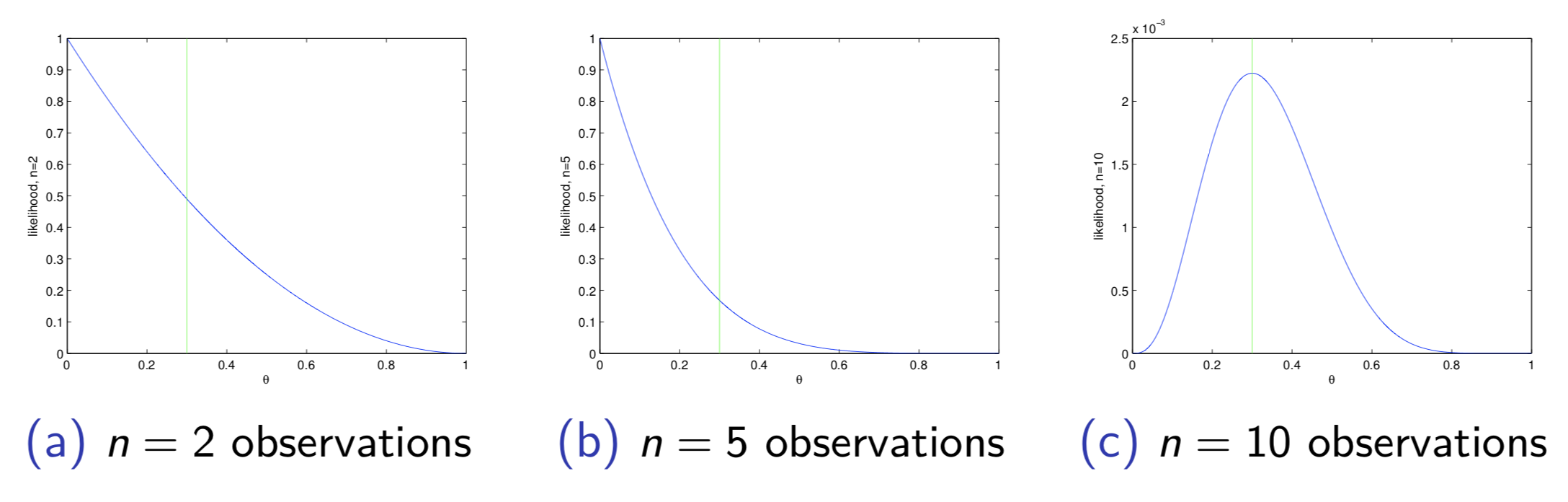
似然函数拥有大量信息，不仅仅是可以用于优化的对象。

我们在求解最大似然函数估计时，仅仅考虑了一个最大值，并未考虑整个（对数）似然函数的形态，事实上
- 如果似然函数有非常强的曲度，最大似然估计是合理的
- 如果似然函数趋近于平滑，取函数上的其他值（其他相近参数），也可以得到相似结果（与观测值的匹配度相近）

学习：贝叶斯推断

$p(\mathbf{x}|\mathbf{\theta}) \overset{data \mathcal D}{\rightarrow} p(\mathbf{\theta};\mathcal{D})$

贝叶斯方法把学习简化为概率推断

利用观测数据决定确定所每一个可能的参数$\mathbf \theta$的合理性，这个合理性通过后验 pdf/pmf 表达，学习和推断在这样的表达下是一致的。
在某些情况下有闭式解(例如Conjugate Prior)；某些情况下，可以使用准确推断(exact inference)方法。
如果没有闭式解，准确推断的计算量庞大，我们可以使用估计推断(approximate inference)，比如采样（sampling）和变分（variational methods）。

后验分布的不同理解

后验分布结合了似然函数和先验
贝叶斯推断考虑了整个似然函数
$\begin{eqnarray} p(\mathbf{\theta}|\mathcal{D}) = \frac{p(\mathbf{\theta},\mathcal{D}) }{p(\mathcal{D})} = \frac{p(\mathcal{D}|\mathbf{\theta}) p(\mathbf{\theta})}{p(\mathcal{D})} \propto p(\mathcal{D}|\mathbf{\theta}) p(\mathbf{\theta}) \propto L(\mathbf{\theta})p(\mathbf{\theta}) \end{eqnarray}$
对于iid数据$\mathcal D = (\mathbf x_1,\cdots, \mathbf x_n)$
$p(\mathbf{\theta}|\mathcal{D}) \propto \Big{[} \prod \limits _{i=1}^n p(\mathbf x_i|\mathbf{\theta}) \Big{]}p(\mathbf{\theta})$
$n$很大的时候，似然函数占据主导位置：$\mathrm{argmax}_{\mathbf \theta}p(\mathbf \theta| \mathcal D) \approx \mathrm{MLE}$ (假设先验分布非零)
后验分布是一个条件分布
考虑离散值数据

$p(\mathbf \theta | \mathcal D) = p(\mathbf \theta | \mathbf x = \mathcal D) = \frac{p(\mathbf \theta , \mathbf x = \mathcal D)}{p(\mathcal D)}$

Conjugate Prior

后验分布例子：高斯，伯努利和所有随机变量可见并为离散值的有向图模型

见附件

附件

Modified 02th-Jun-2018 20:20

Shinoyuki

基于模型学习的基本概念 Basics of Model-based Learning