Recurrent neural network grammars (RNNG)

Recurrent neural network grammars 实现语言的分层形式表达，RNNG中存在的bias为top bias，较符合语言逻辑。

本文介绍了Recurrent neural network grammars (RNNG)的原理，优点和实验结果。

原文参考 Recurrent Neural Network Grammars (Chris Dyer, et al., 2016)

写中文的notes好累啊，所以这篇暂时是英文的 ( ´▽｀)

Intro

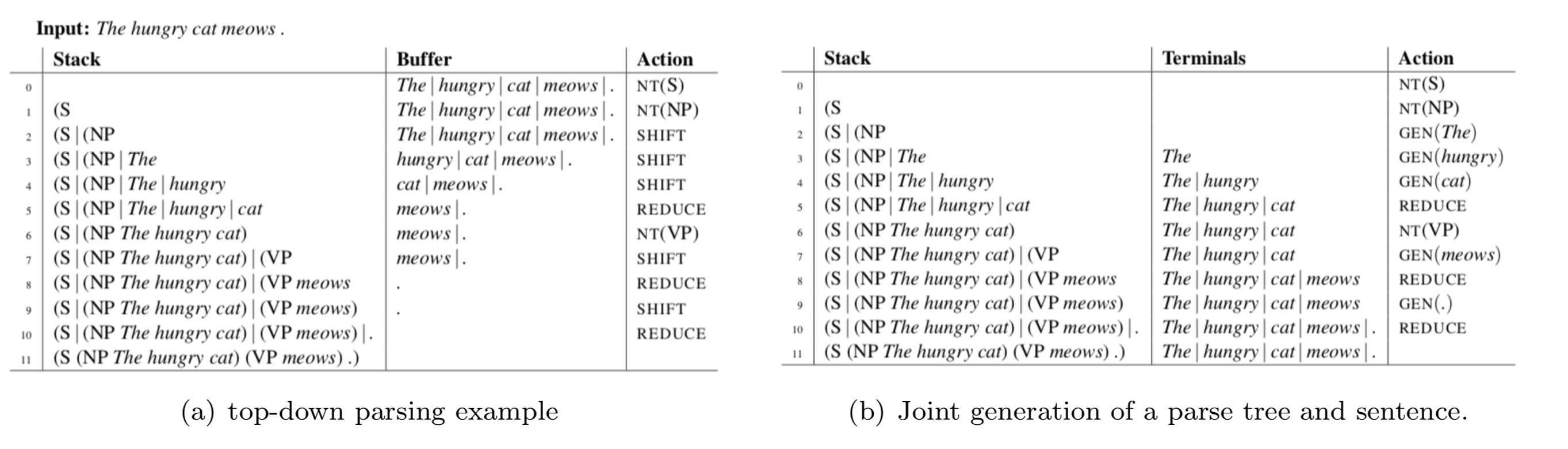
Top-down Parsing and Generation

• Parser Transition
  – bottom-up shift-reduce recognition algorithms
  – the parsing algorithm: mapping from sequences of words to parse trees.
  – Stack($S$): contains terminal symbols, open nonterminal symbols and completed constituents. Begin with empty.
  – Input Buffer(B): contains unprocesses terminal symbols. Begin with complete sequence of words.
  – Info. to train a classifier: current contents on Stack (some part of $y_t$) and Buffer (part of $x_t$)
  – Top-down parsing example Figure 1(a)
• Generator Transitions
  – Algorithm that stochastically generates trees and terminal symbols.
  – Need two changes of parsing algorithm: no input buffer of unprocesses words, rather there is an Output Buffer ($T$)
  – Instead of a SHIFT operation, there are GEN($x$) operations which generate terminal symbol $x \in \Sigma$ and add it to the top of the Stack (S) and the Output Buffer ($T$)
  – Predict action according to a conditional distibution that depends on the current content of $S$ and $T$. when using RNN model, we also use information of past actions. see RNNG

**Figure 1**

RNNG Sturcture

RNNG</font>

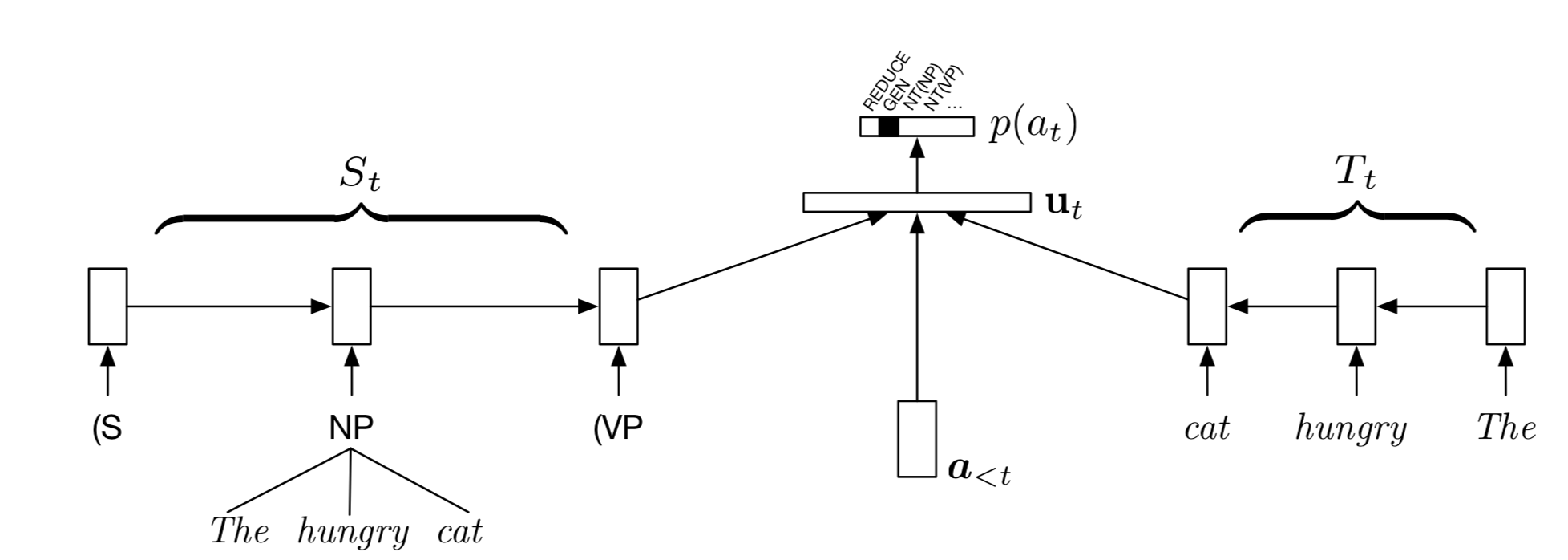
• Generate a set of actions
• at each timestep, we use information: Previous terminal symbols (Tt); Previous actions (a<1); Current
  stack contents (St).
• $T_t, a<t$ could use normal RNNs or any RNN variants; But St is more complicated:
  • The elements of the stack are more complicated objects than symbols from a discrete alphabet: open nonterminals, terminals, and full trees are all present on the stack.
    • Define a new syntactic composition function that recursively defines representations of trees.
  • it is manipulated by push and pop operations.
    • Need a stack LSTMs or RNNs to obtain the representations of $S$ under push and pop operations.

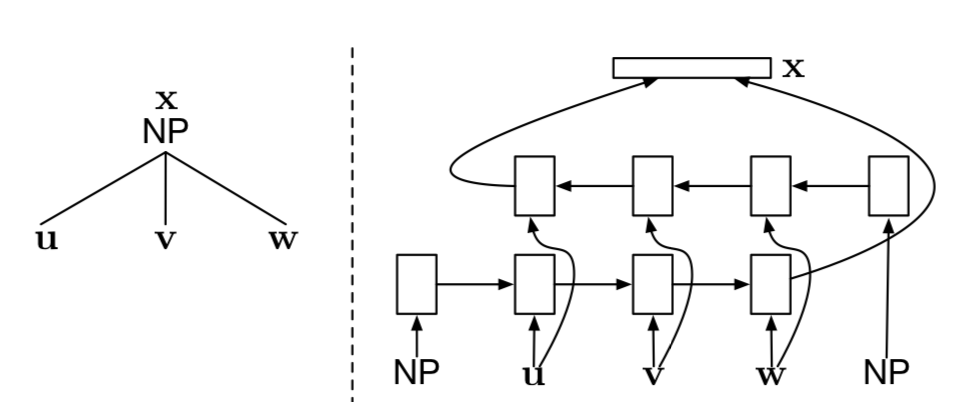
Syntactic Composition Function

• Structure see Figure 2
• Syntactic composition function based on bidirectional LSTMs that is executed during a REDUCE operation:
  • The parser pops a sequence of completed subtrees and/or tokens (together with their vector embeddings) from the stack;
  • makes them children of the most recent open nonterminal on the stack
  • completing the constituent.
• A bidirectional LSTMs based composition function to compute an embedding of this new subtree.

Figure 2: the network on the right models the structure on the left.

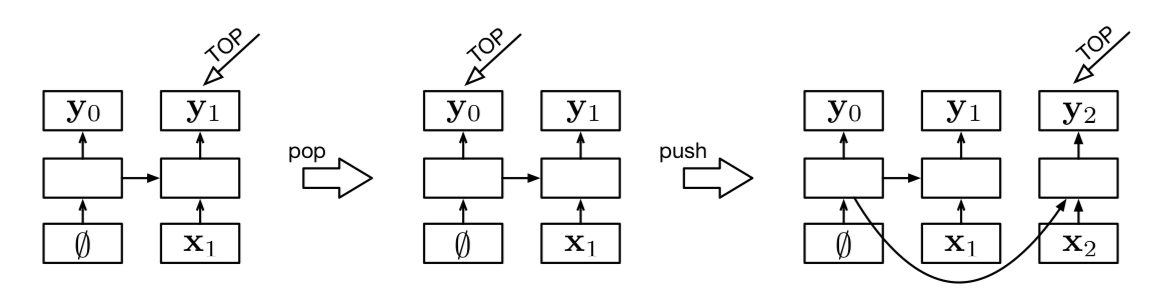
Stack LSTMs or RNNs

• See Figure 3
• A stack LSTM extends a conventional left-to-right LSTM with the addition of a stack pointer (notated as TOP in the figure).
  • the boxes in the lowest rows represent stack contents, which are the inputs to the LSTM
  • the upper rows are the outputs of the LSTM (in this paper, only the output pointed to by TOP is ever accessed)
  • and the middle rows are the memory cells and gates.
• This figure shows three configurations
  • a stack with a single element (left)
  • the result of a pop operation to this (middle)
  • and then the result of applying a push operation (right)
• Arrows represent function applications (usually affine transformations followed by a nonlinearity).

Figure 3: A stack LSTM

Complete RNNG model

• Structure see Figure 4 and Table 1
• ！待编辑，需要比较简洁的演示 Table 1: Line 7

Figure 4: Neural architecture for defining a distribution over at given representations of the stack ($S_t$), output buffer ($T_t$ and history of actions($a_{\ t}$). This architecture corresponds to the generator state at line 7 of Figure 1(b)

Implementation and task

Parameter Estimation

• RNNGs jointly model sequences of words together with a “tree structure’s $p_{\theta}(\mathbf x,\mathbf y)$
• Any parse tree can be converted to a sequence of actions (depth first traversal) and vice versa
  • we use trees from the Penn Treebanck
• We could treat the non-generation actions as latent variables or learn them with RL, effectively making this a problem of grammar induction

Inference of RNNGs

• An RNNG is a joint distribution $p(\mathbf {x},\mathbf {y})$ over strings $\mathbf {x}$ and parse trees $\mathbf {y}$
• Two inference questions:
  • $p(\mathbf{x})$ for given $\mathbf{x}$: Language modeling.
  • $argmax_{\mathbf{y}} p(\mathbf{y}\mid\mathbf{x})$ for a given $\mathbf{x}$: parsing.
• Dynamic programming algorithms we often rely on are of no help here
• Could use Importance Sampling to do both by sampling from a discriminatively trained model: MC integral.

RNNG as a mini-linguist

• Replace composition with one that computes attention over objects in the composed sequence, using embedding of NT for similarity.
  • Idea: to compute representation of NP, we may need to pay more attention on N in that NP.

Summary

• Language is hierarchical, and this inductive bias can be encoded into an RNN-style model.
  • when we’re building a learning model, we do have to build some kind of bias on these models.
  • The licensing context (e.g., not…anybody) depends on recursive structure (syntax)
• RNNGs work by simulating a tree traversal-like a pushdown automaton, but with continuous rather than finite history.
  • it uses continuous representations.
  • simply training on the word sequences and it’s bracketed sequences (trees) does not generate well-formed trees.
  • because there’s no internal mechanism to enforce you’ve got a well bracketed string.
  • traverse the tree also traverse the string.
• Modeled by RNNs encoding previous tokens, previous actions, and stack contents A stack LSTM evolves with stack contents.
• The final representation computed by a stack LSTM has a top-down recency bias, rather than left-to- right bias, which might be useful in modeling sentences.
• Effective for parsing and language modeling, and seems to capture linguistic intuitions about headedness.
  • interesting results: parsing performance of Stack-only RNNG is the best; without Stack info, the system did not work very well on both parsing and LM
    ∗ leaving out stack is harmful
    ∗ using it on its own works slightly better than complete model on parsing.

References

Dyer, C., Kuncoro, A., Ballesteros, M., & Smith, N. A. (2016). Recurrent neural network grammars. arXiv preprint arXiv:1602.07776.

Modified 13rd-May-2018 21:00